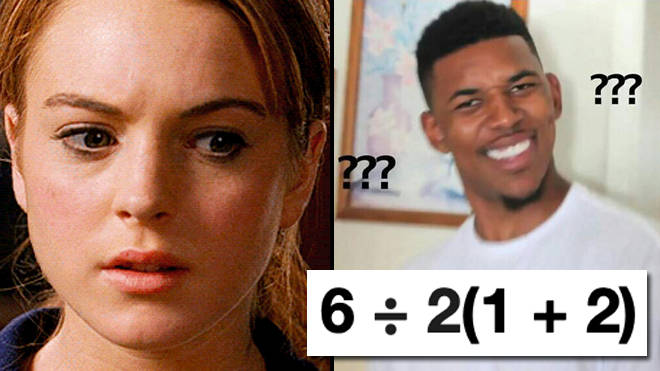বিখ্যাত দুই অংক :
৮÷২(৩+১) … …. …. (রাশি 1)
৬÷২(২+১) … …. .… (রাশি 2)
প্রথমটির উত্তর ১ না ১৬ এবং দ্বিতীয়টির উত্তর ১ না ৯, তা নিয়ে শুধু বাংলাদেশ নয় বরং কয়েক দশক ধরেই বিশ্বের লক্ষ লক্ষ মানুষের মাঝে বিতর্ক রয়েছে। বিশেষ করে বাংলাদেশে যারা ১৬ বা ৯ বলছে, তাদের কাছে যুক্তি আছে । আর যারা ১ বলছে, তাদের ৯৯.৯৯% জানেই না কেন তারা ১ বলেছে । ১ নিয়ে যে যুক্তি তারা দেখায় তা শতভাগ ভুল! আর এ জায়গাটা আসলেই ভয় পাওয়ার মতো কেননা এ তালিকায় ‘শিক্ষক’ মহলের নামও রয়েছে। তাদের ভুলটা কোথায় তা নিয়ে শেষে আলোচনা করবো। তার আগে আসল সমস্যাটা নিয়ে আলোচনা করা যাক।
.
প্রায় বছর দেড়েক আগে শ্রদ্ধেয় গণিতবোদ্ধা, চমক হাসান ভাইয়ের এক পোস্টের পর ৬÷২(২+১) সমস্যাটা পুনরায় আলোচনায় আসে এবং ‘তথাকথিত’ BODMAS নিয়ম নিয়ে আরো একবার গবেষণা হয় । চমক ভাই পুরোপুরি নিরপেক্ষ ব্যাখ্যা দাঁড় করান তবুও উনার রেজাল্টটা অনেকটাই ৯-ঘেঁষা ।
এ জায়গায় কিছু মিসিং লিংক ছিল তা বলবো এবং কেন ৯ বা ১৬ গ্রান্টেড মেনে নেয়া উচিত না তা-ও আমি ব্যাখ্যা করবো (নিঃসন্দেহে চমক ভাইয়ের সাথে আমি কোনোরকম দ্বিমত পোষণ করতে যাচ্ছি না)। তার আগে বলি জনপ্রিয় BODMAS, BEDMAS, BIDMAS বা GEMDAS, এরা হচ্ছে কানাডা, ব্রিটেন, অস্ট্রেলিয়া, এশিয়া, আফ্রিকার । শুধু আমেরিকায় PEMDAS বেশি জনপ্রিয় । PEMDAS মানে Parentheses, Exponent, Multiplication, Division, Addition, Subtraction ।
আমেরিকার বাচ্চারা একে বলে “Please Excuse My Dear Aunt Sally” । এখানে ভাগের আগে গুণ হয় । আমাদের এই লেখার জন্য আমরা BODMAS-এর পরিবর্তে PEMDAS ব্যবহার করব, কারণ ক্যালকুলেটরে PEMDAS ব্যবহার করা হয় আর ঝামেলাটা এখানেই ।
BODMAS/PEMDAS অনুযায়ী :
৬÷২(২+১)
=৬÷২(৩) [এখানে ব্র্যাকেট বা Parentheses আগে]
=৬÷২×৩ [Juxtaposition বা Implicit Multiplication অনুযায়ী ব্র্যাকেট উঠে গেলে গুণ হবে]
.
এখন আসি আসল খেলায় । বাংলাদেশী যারা উত্তর ১ বলেছে তারা ১ বলেছে এই হিসেবে যে,
= ৬÷২(৩)
= ৬÷২ এর ৩ [ ব্র্যাকেট উঠলে ‘এর’ বা ‘of’ ]
= ৬÷(২×৩) [ ভাগের আগে ‘of’-এর কাজ ]
=৬÷৬
=১
.
এই নিয়ম পুরোপুরি ভুল!
Parentheses-উঠলে কখনোই ‘এর’ বা ‘of’ হয় না । গুন হবে Juxtaposition multiplication-এর কারনে, সেটা হোক BODMAS কিংবা PEMDAS । ‘এর’ বা ‘of’ এর প্রয়োগ ৩টি :
–1) Fraction (ভগ্নাংশ যেমন 1 ½ = ⅔ )
–2) Order (Exponent বা Power)
–3) Percentage (শতাংশ)
বুঝাই যাচ্ছে, উপরের ক্যালকুলেশনে ‘এর’ বা ‘of’ এর চিহ্নমাত্র থাকবে না ।
২য় ভুলটা হচ্ছে, তারা বলে BODMAS/BEDMAS অনুয়ায়ী ভাগ আগে, পরে গুণ। তবে তাও শতবছর ধরে বিতর্কিত। গণিতবিদ Florian Cajori তার A History of Mathematical Notations (১৯২৮) বইয়ে উল্লেখ করেন যে আগে গুণ হবে না ভাগ, তা তখনও অমীমাংসিত ।
মূলত, গুণ ও ভাগ একসাথে থাকলে তাদের গুরুত্ব একই, আগে-পরে ফ্যাক্ট না (by Elementary PEMDAS rule, quoted by Oliver Knill, Harvard Math Department) । শুধু Left-to-right হিসাব হবে । PEMDAS নিয়মে আগে গুণ হয়, BODMAS-এ হয় ভাগ।
কিন্তু মার্কিন গণিতবিদ Webster Well-এর First Year Algebra (১৯১২) বই কিংবা Frank C Touton, Herbert Hawkes, W.A. Luby-এর First Course Algebra (১৯২৫) বইতে স্পষ্টত যোগ-বিয়োগ কিংবা গুণ-ভাগ একসাথে থাকলে বাম-থেকে-ডান করার নির্দেশ রয়েছে । এবং এর সমর্থনে বর্তমানে অসংখ্য প্রমাণও রয়েছে । তাই BO(DM)(AS) বা PE(MD)(AS) উভয়েই পরের হিসাবটা হবে :
= ৬÷২×৩
=৩×৩ [ Left-to-Right ]
= ৯
যদিও বাংলাদেশীদের হিসাবটা ঠিকই ছিল কিন্তু পদ্ধতিটা ভুল ।
এখন কেন quantity-1 ও 2 (১, ২নং রাশি) এর উত্তর একেক ক্যালকুলেটরে একেক রকম আসে?
মূলত ঝামেলাটা হচ্ছে ২(২+১) ও ২(৩+১) এই পার্ট নিয়ে। গণিতবোদ্ধাদের একটা বড় অংশ বলছেন,
২(১+২) যখন
= ২(৩) হবে তখন ব্র্যাকেটের আগে কোনো অপারেটর (যোগ, বিয়োগ, গুণ, ভাগ) না থাকায় Juxtaposition অবস্থার সৃষ্টি হবে যা Implicit Multiplication-এর কারনে :
=২(৩) থেকে (২*৩) তে আগে কনভার্ট হবে, পরে ৬ থেকে ভাগ করতে হবে । প্রকৃতপক্ষে, শত শত বছর ধরেই গণিবিদ, বিজ্ঞানী ও প্রকৌশলীরা এই Juxtaposition ব্যবহার করে আসছেন এবং তাদের প্রায় সবাই একে গুণ-ভাগের চেয়েও উপরে স্থান দেন । তাই PEMDAS হয়েছিল PEJMDAS (পেজমদাস) এবং BODMAS হয়ে গেল BOJDMAS । তবে কেউই বিষয়টা Explicitly উল্লেখ করে যাননি, এদের নামও দেননি ।
.
PEMDAS-এর অস্তিত্ব পাওয়া যায় ১৯০০ সাল থেকেই। এর সাথে Juxtaposition-এর কাজও করা হতো (যেমন—ব্র্যাকেটের সাথে কিছু না থাকলে গুণ ধরা) তবে তাকে আলাদাভাবে উল্লেখ করার প্রয়োজন কিন্তু মনে করেনি কেউই । এই অস্পষ্টতা বা Ambiguity-ধরা পরে আরো পরে । তবে BODMAS/PEMDAS-কে অঘোঘিত BOJDMAS/PEJMDAS ধরার পক্ষেই সবচেয়ে বেশি রেফারেন্স পাওয়া যায় ।
যেমন—American Institute of Physics (AIP) Style Guide-এর ২৬ পৃষ্ঠায় 1/3x কে 1/(3x) লিখতে নির্দেশ দেয়া হয় (চাইলে গুগলেও দেখতে পারেন) । অর্থাৎ PEJMDAS-এর ব্যবহার যে প্রচলিত ছিল তার প্রমাণে কোনো সন্দেহ নাই ।
১৯৭০-৮০র দশকে TI (Texas Institute) calculator যেমন TI-80, TI-81, TI-85 ইত্যাদি ও CASIO ক্যালকুলেটরগুলোর (২০০১ এর FX-570MS ও পূর্ববর্তী সব) সবই PEJMDAS মেনে চলতো যেখানে 1, 2 নং রাশির মান :
৬÷২(৩)
= ৬÷(২×৩) [Implicit Multiplication/Juxtaposition মেনে which comes before Division-Multiplication]
= ৬÷৬
= ১ দেখাবে ।
পরবর্তীতে TI-83 PLUS, TI-89, TI-Nspire ইত্যাদি ভার্সনে Juxtaposition ও গুণ-ভাগকে এক কাতারে ফেলা হয় অর্থাৎ PEMDAS নিয়মে বাম-থেকে-ডান । আর ২০১৮ সালে CASIO নিজস্ব বিবৃতিতে বলে যে, অনেক North American স্কুল-হাই স্কুল শিক্ষক ও গণিকপ্রেমীদের উৎসাহে ২০০৫ সালে fx-ES series ক্যালকুলেটর(যেটা এদেশে প্রচলিত) দিয়ে PEMDAS নিয়মে সুইচ করে ।
পরবর্তীতে তারা আবার ২০০৮ সালেই FX-ES PLUS series-দিয়ে আগের সেই PEJMDAS নিয়মে ফিরে যায় যেখানে ব্র্যাকেটের পর Implicit Multiplication-কে গুণ-ভাগের চেয়েও Top priority দেয়া হয় । অত্যাধুনিক fx-100AU PLUS ক্যালকুলেটরে ৬÷২(২+১) লিখলে অটোমেটিক ৬÷(২(২+১)) এই এক্সট্রা ব্র্যাকেট এসে যায় ! দারুন না !!
যেমন :
6/2x = (6/2)*x [আধুনিক PEMDAS/BODMAS]
আবার 6/xy = 6/(xy) [Conventional PEJMDAS]
.
তবে WolframAlpha ব্যতিক্রম নিয়মে PEJMDAS-কে সমর্থন করে ।
x/x/x কে Left-to-Right নিয়মে লিখে (x/x)/x
আবার x^x^x কে Right-to-Left নিয়মে লিখে x^(x^x)
Exponent বা Power-এর ক্ষেত্রে Wolfram-এর ধারনাটা সঠিক । কেননা আমরা যখন log(log(logx)) বা g(h(x)) লিখি, আমরা ডান থেকে বামে কিংবা ভিতর থেকে বাইরে যাই ।
.
এখন আমরা কোনটা মেনে চলবো ?
আগেই বলেছি, বিংশ শতাব্দী পর্যন্ত অসংখ্য গণিতবিদ (বলতে পারেন মেজরিটি অংশ) অবচেতন মনেই Juxtaposition মেনে PEJMDAS/BOJMDAS অনুযায়ী পাটিগণিত ও বীজগণিত করতো (একই সাথে Left-to-Right নিয়মকেও অনেকে সমর্থন করতো) । PEMDAS-এর বিতর্কটা সবচেয়ে বেশি আসে বিংশ শতাব্দীর শেষ থেকে, তাও North American স্কুল শিক্ষকদের প্রভাবে, কোনো প্রসিদ্ধ গনিতবিদ বা ইঞ্জিনিয়ারের রিসার্চের ফলে নয়!
সেখানে তারা Juxtaposition-কে গুরুত্ব না দিয়ে গুণ-ভাগের মতো একই কাতারে ফেলে এবং Left-to-Right নিয়ম ফলো করে । অর্থাৎ আসল প্রশ্নটা হলো Juxtaposition ব্যবহার হবে কি-না তা নিয়ে, গুণ-ভাগের সিক্যুয়েন্স নয় । কারণ তা এক বাক্যে Left-to-Right ।
.
তাছাড়া আমরা নিজেরাও অজান্তেই বছর বছর PEJMDAS/BOJDMAS কে ফলো করে আসছি । যেমন :
১÷২√৩ কে কিভাবে লিখবো ?
(1) (১/২)×√৩ = ০.৮৮৬ [ অধুনা PEMDAS নিয়ম ] নাকি,
(2) ১÷(২×√৩) = ০.২৮৯ [ Conventional PEJMDAS নিয়ম ]
নিঃসন্দেহে ২নং নিয়মটাই ফলো করা হয় বেশি (অথবা সবসময়ই)।
.
আবার 2X/3Y-1 কে কিভাবে হিসাব করি ?
(1) (2x/3)(y-1) [ অধুনা PEMDAS ]
(2) {(2x)/(3y)} – 1 [ Conventional PEJMDAS ] নাকি
(3) (2x)/(3y-1) [বিধি বহির্ভূত]
এখানেও আমরা সচরাচর ২নং-টাকেই বেশি গ্রহণ করে থাকি! অর্থাৎ শুধুমাত্র স্কুল শিক্ষকদের পছন্দে উত্তর আমেরিকার PEMDAS বা সমমানের BODMAS, বহু পুরোনো Juxtaposition-কে বাদ দিয়ে যে নতুন নিয়ম চালু করেছে, অনেকেই এর বিরোধিতা করেছে ।
যদিও কিছু কিছু ক্ষেত্রে Juxtaposition ছাড়াই আধুনিক PEMDAS নিয়ম শতভাগ সঠিক উত্তর দেয় (যেমন রাশি-1 ও রাশি-2) তবে সব সময় হয় না (যেমন উপরের ২ টা উদাহরণই)। তাই অধুনা North American PEMDAS পুরোপুরি গ্রান্টেড নয় ! এমনকি আধুনিক গনিত লেখক Robert B Ash, তার Basic Abstract Algebra বইতেও Conventional PEJMDAS-কে সমর্থন করেছেন (গুগল করেও দেখতে পারেন)।
তাই মেশিন ও মানুষ, ২ ভিন্ন ভিন্ন সত্তা যে হিসাব করবে তার ফলাফল অবশ্যই ভিন্ন আসবে । এ ক্ষেত্রে যা মাথায় রাখতে হবে:—
(1) ব্র্যাকেট উঠলে গুণ বসবে এবং তার গুরুত্ব গুণ-ভাগের চেয়ে বেশি হবে ও আগে সমাধান করতে হবে Juxtaposition/Implicit Multiplication এর জন্য (‘এর’ বা ‘of’ এর জন্য নয়) ।
(2) ঐতিহাসিকভাবে PEMDAS নিয়মে আগে গুণ, BEDMAS/BODMAS-এ আগে ভাগ করা হয় । তবে বর্তমানে গুণ-ভাগ পাশাপাশি থাকলে গুরুত্ব এক ও Left-to-Right ।
(3) লেখক N.J. Lennes-এর মতে ‘/ বা slash’ ও ‘÷ বা Obelus’ ভিন্ন অর্থ বহন করে এবং ব্যবহারে সাবধান হওয়া উচিত ।
(4) Ambiguity ও বিতর্ক দূরীকরণে ব্র্যাকেট ব্যবহার করতে হবে ।
.
যেমন : ১৮/৩×২
— এটার মানুষের দেয়া উত্তর ৩, কারণ তারা আদিম PEMDAS ফলো করে ।
— আবার মেশিনের দেয়া উত্তর ১২, কারণ সেটা উপরের নিয়ম ফলো করে (বাম থেকে ডান) ।
— আদিম ও আধুনিক দুই BODMAS নিয়মেই ১২ হয় ।
— আবার আধুনিক PEMDAS নিয়মেও ১২ হয় (ঝামেলাটা বুঝা যাচ্ছে না কারণ Juxtaposition নেই)
.
আবার ৮÷২(৩+১)
–এটার মানুষের দেয়া উত্তর ৮÷২(৪) = ৮÷(২×৪)=৮÷৮=১, যা শতভাগ সঠিক কারণ তা উপরের সব নিয়ম ফলো করে (Conventional PEJMDAS) ।
–আবার মেশিনের দেয়া উত্তর ৮÷২(৩+১) = (৮÷২)×(৪)=১৬, যা ১ম নিয়মটি অনুসরণ করেনি (অধুনা PEMDAS) । এটিও ভুল নয়
–আবার যেসব মেশিন/ক্যালকুলেটর তা ফলো করে (Conventional PEJMDAS), তারা ঠিকই ১ দেখাবে । সেটাও সঠিক । শুধু মেথডটা ভিন্ন । তবে উত্তর ‘১’ টা সবচেয়ে বেশি গ্রহণযোগ্য কারন Implicit Multiplication বহু গণিতবিদ অনুসরণ করেছেন এবং তা বাদ দেয়ায় PEMDAS, BODMAS নিয়মেরও সমালোচনা হয়েছে । এই বিষয়টি আজও Ambiguous বা অস্পষ্ট (অমীমাংসিত) ।
.
তাই কেউ যদি রাশি-1 ও রাশি-2 এর অংক দেয় তাহলে উত্তর দিতে হবে ৫টা :
— JUXTAPOSITION RULES ছাড়া :[৮÷২×৪] এবং [৬÷২×৩]
(1) আদিম PEMDAS মানলে উত্তর ১ ও ১
(2) অধুনা PEMDAS মানলে উত্তর ১৬ ও ৯
(3) আদিম BODMAS মানলে উত্তর ১৬ ও ৯
(4) অধুনা BODMAS মানলে উত্তর ১৬ ও ৯
.
— JUXTAPOSITION RULES সহ :[৮÷(২×৪)] এবং [৬÷(২×৩)]
(5) আদিম ও আধুনিক BODMAS/PEMDAS সবসময়ই উত্তর ১ ও ১
আমি 5-কে সমর্থন করি । আপনি?